Сравнение величин в процентах
Иногда бывает удобным сравнивать две величины не по разности их значений, а в процентах. Например, цену двух товаров сравнивать не в рублях, а оценивать, насколько цена одного товара больше или меньше цены другого в процентах. Если сравнение по разности вполне однозначно, то есть всегда можно найти, насколько одна величина больше или меньше другой, то для сравнения в процентах нужно указывать, относительно какой величины вычисляется процент. Такое указание, впрочем, необязательно в том случае, когда говорят, что одна величина больше другой на число процентов, превышающее 100. В этом случае остаётся только одна возможность вычисления процента, а именно деление разности на меньшее из двух чисел с последующим умножением результата на 100.
Формула сложных процентов по вкладам

Сложные проценты используются банками не только для получения выгоды от кредитования. Формат начислений применяется и при оформлении вкладов, тем самым определяя выгоды для инвесторов. Итоговую сумму вклада можно рассчитать используя следующую формулу:
S = D * (1 + % * i / Y / 100 ) * N
Для расчета прибыли по вкладу эффективно использовать другие формулы:
Sp = S — D = D * (1 + % * i / Y / 100 ) * N – D
или
Sp = D * (( 1 + % * i / Y / 100 ) * N — 1)
Для сравнения прибыльности по вкладам, которые оформлены на разный период и для каждого из которых свойственна своя ставка сложных процентов, формула будет выглядеть иначе. Она позволит определить процент, который получит инвестор после капитализации.
P1 = 100 * ((1 + % * i / Y / 100) * N — 1), где:
- D — размер первичного вклада.
- S — общая сумма вклада с начисленными процентами.
- % — процентная ставка.
- Sp — доход.
- N — количество начислений.
- i — количество дней по начислению процентов.
- Y — дни в году.
Итоговая ставка банка, рассчитанная с учетом капитализации процента, называется эффективной. Финансовые институты не учитывают день окончания партнерства, если используют сложную схему начисления прибыли.
Пример использования простых процентов
Условие задачи № 1
Клиент обратился в банк с просьбой о размещении вклада со сроком на полгода. Для 6 месяцев депозита предусмотрена ставка 8,7 % годовых с ежемесячным начислением. Минимальная сумма для совершения сделки: 30 000 рублей.

Итак, взаимодействуя с банком на предъявленных условиях, получаем:
Сумма процентов = 30 000 х 181 х 8,7 : (100 х 365) = 1294,3 руб. Надо отметить, что расчет годового процента по кредиту выглядел бы совершенно таким же образом.
Но в связи с тем, что в условии сказано о ежемесячной выплате процентов, полученная сумма будет осуществлена шестью платежами. Количество календарных дней влияет на размер этих самых выплат. Допустим клиент обратился в декабре, тогда:
- Проценты за декабрь, январь, март, май = 30 000 х 31 х 8,7 : (100 х 365) = 221,67 руб.
- Проценты за февраль = 30 000 х 28 х 8,76 : (100 х 365) = 200,22 руб.
- Проценты за апрель = 30 000 х 30 х 8,7 : (100 х 365) = 214,52 руб.
В итоге за 6 месяцев сумма депозита или кредита с начисленными процентами составит:
Сумма с процентами = 30 000 х (1 + 181 х 8,7 : (100 х 365)) = 31 294,274 руб. Или просто 30 000 + 1294,3 = 31 294,3 руб.
Расчет простых процентов
Для расчета нужно знать какова сумма займа, на какой срок выдаются деньги, по какой ставке, как уплачивается процент. Процентные платежи проводятся каждый месяцев или раз в квартал. Иногда расчет по кредиту не указан по договору.
По какой формуле производится расчет?
% по кредиту = тело займа * %/количество дней в году * дни пользования займа
Для наглядного расчета рассмотрим пример. Олег взял кредит в размере 10 тысяч рублей на срок двадцать дней. Ставка по займу в день 1,7 %. Всего в году 365 дней.
Для расчета годовой ставки необходимо умножить проценты по договору в день на число дней году: 1,7* 365 = 730. Ставка в год равна 620,5 %. Переходим к расчету процентов:
(10 000* двадцать дней * 2 %)+4 000 (% за период)= 4 000 (сумма процентов)
Расчет сложных процентов
Кроме простых процентов, начисляются и сложные. Их расчет производится в случае, если клиент не может выплачивать задолженность в установленный срок, например, помесячно. В следующем периоде на остаток будет начислен фиксированный процент и плюс неуплаченный. Сложный процент применяется по договору между сторонами, которые занимаются предпринимательством.
По какой формуле рассчитываются?
Подсчет производится следующим образом: перемножаем суммы займа на величину, которая равна (1+r)*n. R – ставка по займу (выражается в долях), n – количество платежей по долгу, которые уже прошли.
Рассмотрим пример, клиент получил десять тысяч рублей под 7 % ежемесячно. После получения задолженности проходит 365 дней. Долг будет рассчитан следующим образом:
10 000* (1+0,07)*12 месяцев= 10 000 рублей* 12,8= 128 400 рублей. Размер долга увеличивает, если увеличивается срок пользования.
Кредитная карта Тинькофф Платинум Получите кредитную карту, не выходя из дома Подробнее
Простые проценты по кредиту: формула
Процент по кредиту – это сумма, которую клиент банка выплачивает ему за пользование его средствами. При возврате взятого у банка займа, внесенная сумма превысит изначально полученную на оговоренное число процентов.
Размеры начислений, их периодичность, прочие условия вносятся в кредитный договор, который заключается между сторонами при получении займа. Сумма процентов, причитающихся банку, зависит от условий, на которых выдается кредит:
- годовая процентная ставка;
- будет ли проводиться капитализация процентов;
- срок действия договора;
- как будут выплачиваться проценты.
Капитализация процентов означает то же понятие, что и при расчете вклада, но в депозите при каждом новом начислении расчет идет от базы, которая увеличивается. Если применять одно и то же количество процентов к сумме долга, который становится все меньше с каждым платежом, то и процентные начисления по мере выплаты долга будут становиться все меньше. Такая схема расчетов называется начислениями со сложным процентом.

Простым же процентом в этом случае считается схема, по которой начисления проводятся исходя из фиксированной базы, то есть выплата процентов в предыдущем периоде не оказывает влияния на сумму, по которой вычисляется процент. То есть, простые проценты – это одинаковое количество денег, которое регулярно прибавляется к платежу.
То есть, ежегодно к телу кредита прибавляются процентные начисления, которые были рассчитаны на основе суммы первоначального долга.
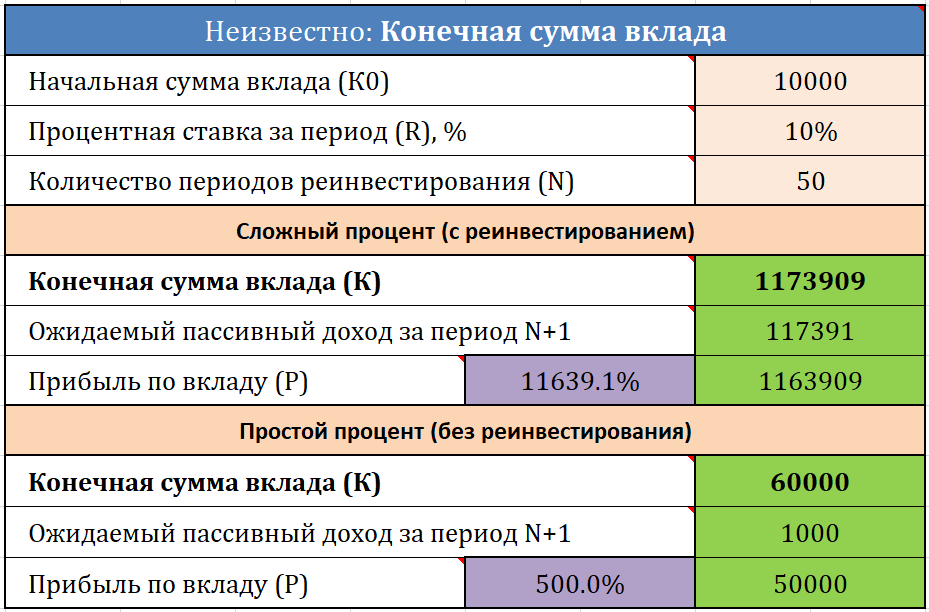
Калькулятор сложных процентов в Excel
Конечно же, задачи на сложные проценты целесообразнее решать в MS Excel по уже известным вам из предыдущих разделов формулам. По ходу статьи вы уже могли скачать некоторые примеры типичных задач, но если этого мало — предлагаю полную подборку калькуляторов по сложным процентам, реализованную в одном Excel-файле. Получить его можно бесплатно, просто заполните форму ниже:
Если письмо не пришло, проверяйте папку «Спам», иногда попадает туда. Если не видите форму подписки, оставьте комментарий к статье и я добавлю ваш электронный адрес вручную.
Вот какие задачи по простым и сложным процентам может решать «Коллекция калькуляторов для инвестора»:
- расчёт конечной суммы вклада;
- расчёт начальной суммы вклада;
- расчёт необходимой процентной ставки;
- расчёт срока инвестирования;
- расчёт конечной суммы вклада с учётом регулярных пополнений и капитализацией;
- ожидаемый пассивный доход в каждом из случаев.
Пример одного из калькуляторов для расчёта сложных процентов в Excel:
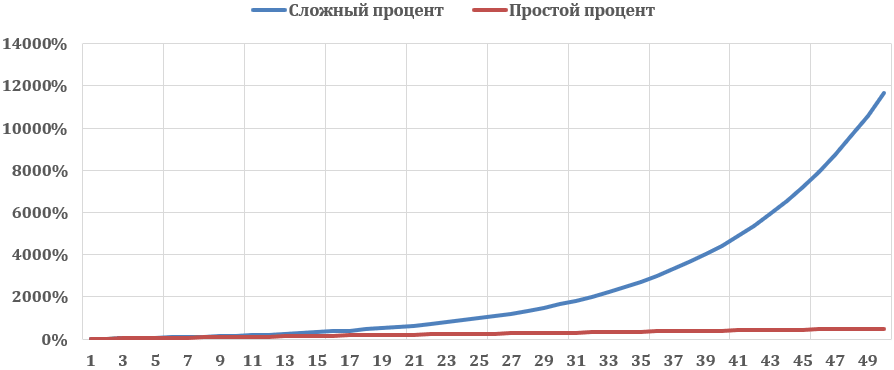
Дополнительно к каждому калькулятору автоматически строится график доходности вклада с капитализацией и без:
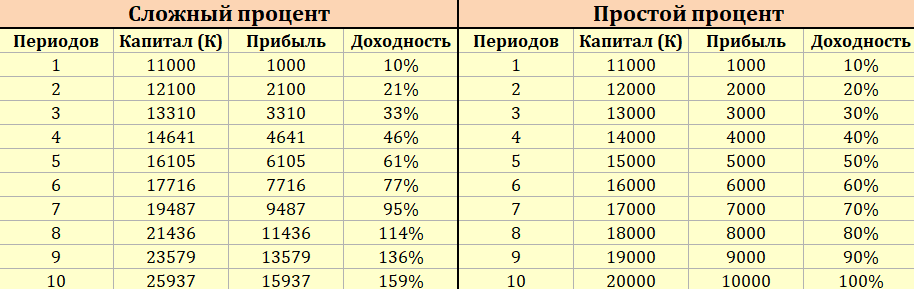
А также уже знакомые вам таблицы:
Думаю, файл будет полезен и для практического использования, и в обучающих целях — в готовом виде есть все формулы, по которым можно считать сложные проценты в Excel.
Капитализация при инвестировании в валютные рынки
Капитализация процентов встречается не только в банке, но и на валютном рынке «Форекс». Инвесторы, отдающие свои капиталы в доверительное управление, получают возможность следить за увеличением своих депозитов в геометрической прогрессии. Специфика данного вида инвестирования в том, что при получении прибыли она не снимается сразу, а распределяется по окончании торгового периода. На протяжении торгового периода, который может составлять неделю, месяц и даже несколько месяцев, будет автоматически проводиться начисление сложных процентов в силу специфики торговли. Для точного расчета дохода не подойдет формула сложных процентов по вкладам. Причина в отсутствии стабильной ставки. Прибыль определяется качеством торговли управляющего, его стратегией и политикой мани-менеджмента, прочими параметрами торговой системы.
Виды процентных ставок по вкладам в банках
Открывая депозит в банке, у вас есть возможность решить, что вы хотите делать с начисляемыми дивидендами – выводить их на карту или прибавлять к сумме первоначального вклада, тем самым капитализируя его. В зависимости от того, какой вариант вы выберете, такой будет и формула расчета процентов. Если вы хорошо помните школьную математику, то вы знаете, что проценты бывают простыми, а бывают сложными.
Как начисляются простые проценты?
Итак, простая ставка по депозитам рассчитывается следующим образом:
Для удобства понимания давайте разберем такой пример: вы открываете в банке депозит на сумму в 50 000 рублей на 1 год с простым начислением процентов. Ставка % составляет 11,5%. Пользуясь вышеуказанной формулой, получается, что через год, после того как будет закрыт ваш депозит, вы заработаете:
В данном случае проценты не будут прибавляться к телу депозита, а каждый месяц (раз в полгода или раз в год) будут выводиться на другой ваш счет. Очень выгодно в таком случае пользоваться ежемесячным выводом процентов на дебетовые карты с начислением процентов на остаток. Если вы не успеваете потратить заработанные на депозите средства, на них будет начислен % по вашей карте.
Как начисляются сложные проценты?
Расчет сложных процентов по вкладу несколько сложнее и интереснее. Однако, прежде, чем мы приступим к его изучению, я предлагаю вам выяснить, в каких случаях мы имеем дело со сложной ставкой.
Открывая в банке депозит, вы вправе решать, прибавлять к нему полученные проценты или выводить их на другой счет. В случае, если вы выбираете первый вариант, по вашему вкладу начисляется сложный процент. То есть, в каждом последующем периоде % начисляются на большую сумму, нежели в предыдущем, тем самым ускоряя рост размера депозита.
Это присоединение выплат по депозиту к первоначальной сумме вклада очень важно, поскольку сумма накоплений растет все быстрее и быстрее. Причем, моделью роста выступает не арифметическая прогрессия, а экспонента
Для сравнения давайте возьмем расчет простых и сложных процентов по одному и тому же вкладу. Условно положим на счёт 100 000 рублей под 10% годовых. В конце расчетного периода по простой ставке мы получим:
100 000 * 10 / 100 = 10 000 рублей;
Чтобы посчитать доходность вкладов с капитализацией выведем общую формулу:
Формула сложных процентов представлена ниже:
Переменные означают следующее,
Рассчитываем наш пример:
100 000 * (1+0,833*365 / 100*365)^12 = 10 466,92 рублей
Таким образом, один и тот же депозит, положенный в банк на разных условиях, может принести как 10 000 рублей чистой прибыли, так и 10 466 рублей.
В последнем случае мы имеем дело с капитализацией депозита – добавлением начисленных % к телу депозита. Как результат, получаем рост первоначальной суммы инвестиции и начисление % на увеличенную сумму.
Чтобы не считать доходность депозита вручную, советую вам воспользоваться калькулятором сложных процентов. В нем вы сможете указать суммы регулярных довложений за определенный период. Найти такой калькулятор можно на моем сайте с правой стороны, в сайдбаре, во вкладке «Калькулятор доходности».
Как начисляется эффективная ставка?
Ну а теперь давайте разберемся с эффективной процентной ставкой по депозиту, чтобы собрать в голове полную картинку банковских предложений.
Эффективной ставкой принято называть ставку, дающую равнозначный доход по идентичному депозиту без капитализации процентов. То есть, предположим, что вы открываете счёт в размере 50 000 на год под 8% годовых с условием капитализации. Проводим расчет по уже известной нам формуле и получаем:
50 000 * (1+0,6666*365/100*365) 12 = 54 150 рублей.
А теперь смотрим на предложение в соседнем банке. Здесь вы можете открыть тот же самый депозит, но без капитализации, зато под 8,3% годовых. Такое предложение позволит вам получить точно такой же доход, как в случае с капитализацией.
(50 000 * 8,3 * 365/365) / 100 = 4 150 рублей.
Чтобы быстро рассчитать эффективную ставку по депозиту, достаточно сделать следующее:
Именно эти 8,3% и являются нашей эффективной годовой ставкой по депозиту с ежемесячной капитализацией. То есть, если вклад без прибавления процентов к телу депозита будет иметь ставку, превышающую 8,3%, то такое вложение будет для нас более выгодно, нежели депозит с 8% годовых и ежемесячной капитализацией. Не забываем, что в случае с вкладом с 8.3% годовых, ежемесячный процент можно перевести на дебетовую карту с начислением на остаток, в этом случае этот вклад будет выгоднее.
Простые проценты
На практике применяются три варианта расчета простых процентов:
- точные проценты с точным числом дней ссуды (английская практика). Обозначается как 365/365 или АТС/АТС.
- обыкновенные (коммерческие) проценты с точным числом дней ссуды (французская практика). Обозначается как 365/360 или АТС/360.
- обыкновенные проценты с приближенным числом дней ссуды (германская практика). Обозначается как 360/360.
По схеме 360 количество дней к году принимается равным 360 (в каждом месяце по 30 дней).
Пример. Определить приближённое число дней между 12.02.2019 и 27.08.2020.
Если год рассматривается как промежуток, содержащий 12 месяцев продолжительностью 30 дней (дивизор равен 360 дней), то приближённое число дней рассчитывается следующим образом:
где y – номер года, m – номер месяца в году, d – номер дня в месяце.
n = 360*(2020-2019)+30*(8-2)+(27-12) = 555 дней
Pin
Когда срок финансовой сделки не равен целому числу лет:
S=P·(1+tT·i)
где t – срок в днях, T – временная база (365 или 360)
Примеры задач на простые проценты
Решить
- Ссуда в размере P = 1 млн.руб. выдана d1 = 20.01 до d2 = 05.10 включительно под i = 18% годовых. Какую сумму должен заплатить должник в конце срока при начислении простых процентов? При решении применить три метода расчёта срока ссуды.
Начальная дата: 20.01, конечная дата: 05.10, количество дней между датами: 258
Январь, 11 дней: с 21.01 по 31.01
Февраль, 28 дней: с 01.02 по 28.02
Март, 31 день: с 01.03 по 31.03
Апрель, 30 дней: с 01.04 по 30.04
Май, 31 день: с 01.05 по 31.05
Июнь, 30 дней: с 01.06 по 30.06
Июль, 31 день: с 01.07 по 31.07
Август, 31 день: с 01.08 по 31.08
Сентябрь, 30 дней: с 01.09 по 30.09
Октябрь, 5 дней: с 01.10 по 05.10
Итого: 11 + 28 + 31 + 30 + 31 + 30 + 31 + 31 + 30 + 5 = 258
S=P·(1+tT·i)
1) Точные проценты с точным числом дней ссуды (365/365)
S=1 000 000·(1+258365·0.18)=1 127 232.88 руб.
2) Обыкновенные проценты с точным числом дней (365/360)
S=1 000 000·(1+258360·0.18)=1 129 000 руб.
3) Обыкновенные проценты с приближённым числом дней (360/360)
Количество дней между датами: 255
Январь, 10 дней: с 21.01 по 30.01
Февраль, Март, Апрель, Май, Июнь, Июль, Август, Сентябрь по 30 дней
Октябрь, 5 дней: с 01.10 по 05.10
Итого: 10 + 30*8 + 5 = 255
S=1 000 000·(1+255360·0.18)=1 127 500 руб. - Через d = 180 дней после подписания договора должник уплатит S = 310 тыс.руб. Кредит выдан под i = 16% годовых. Какова первоначальная сумма долга при условии, что временная база равна 365 дням?
P=S(1+tT·i)
Находим современную стоимость P=310 000(1+180365·0.16) = 287 328.59 руб.
Простые проценты по кредиту: формула
Процент по кредиту – это сумма, которую клиент банка выплачивает ему за пользование его средствами. При возврате взятого у банка займа, внесенная сумма превысит изначально полученную на оговоренное число процентов.
Размеры начислений, их периодичность, прочие условия вносятся в кредитный договор, который заключается между сторонами при получении займа. Сумма процентов, причитающихся банку, зависит от условий, на которых выдается кредит:
- годовая процентная ставка;
- будет ли проводиться капитализация процентов;
- срок действия договора;
- как будут выплачиваться проценты.
Капитализация процентов означает то же понятие, что и при расчете вклада, но в депозите при каждом новом начислении расчет идет от базы, которая увеличивается. Если применять одно и то же количество процентов к сумме долга, который становится все меньше с каждым платежом, то и процентные начисления по мере выплаты долга будут становиться все меньше. Такая схема расчетов называется начислениями со сложным процентом.

Простым же процентом в этом случае считается схема, по которой начисления проводятся исходя из фиксированной базы, то есть выплата процентов в предыдущем периоде не оказывает влияния на сумму, по которой вычисляется процент. То есть, простые проценты – это одинаковое количество денег, которое регулярно прибавляется к платежу.
То есть, ежегодно к телу кредита прибавляются процентные начисления, которые были рассчитаны на основе суммы первоначального долга.
Формула расчета простых процентов
Формула расчета процентов по кредиту аннуитет достаточно сложная. По своей сути такие платежи включают не только основной долг, но и ставку на оставшуюся сумму главного займа. Со временем сумма главного долга становится меньше, а значит и размер суммы, начисляемой на нее, существенно снижается. Итак, для вычисления суммы основного долга можно использовать такую формулу:
ВД=ПСК/СК
Где ПСК – первоначальный размер средств, взятых в займы, СК – термин, на который все эти средства берутся, ВД является возвратом основного долга. После этого можно использовать формулу расчета простых процентов по кредиту. Интересно, что позиции финансовых учреждений, касательно подсчета, достаточно разные. В принципе, все зависит от того, на какой период вы оформляете соглашение.
12 месяцев = один год — позиция №1. Формула будет выглядеть таким образом:
СНП= ООД*ПГС/12
Где ООД является остатком основного долга, что существует на момент расчета, ПГС –ставка (годовая), СНП – ставка, что начисляется.
365 дней = один год — позиция №2. Формула будет выглядеть таким образом:
СНП = ООД*ПГС*КДМ/365
Где ООД является остатком основного долга, что существует на момент расчета, ПГС –ставка (годовая), КДМ – календарные дни в 1 месяце (как правило, от 28 до 31) ,СНП – ставка, что начисляется.
Банковские расчёты
Банки иногда используют другие формулы для определения прибыли по разным вкладам. Такая формула подразумевают более сложный и точный расчёт. В случае с простой ставкой она выглядит, как S = P * I * t /K. В ней:
- s — объём начисленных процентов;
- p — размер взноса;
- I — процентная ставка за год, разделённая на 100%;
- t — количество дней, за которые начисляется прибыль;
- k — число дней в году.
Пусть размер вклада равен 100 тысяч рублей, срок — 181 день, а годовая ставка — 7%. В день его закрытия вкладчик получит доход в размере 100 000 x 0,07 x 181 / 365 = 3 471,23 рублей.
Для сложной ставки применяется выражение S = P * (1 + I * j / K) n — P. Помимо указанных выше параметров, здесь дополнительно используется j — календарные дни в периоде, в течение которого осуществляется капитализация по вкладу, и n — периодичность начисления.
Если к аналогичным исходным данным добавить n = 2 и j = 90, получится, что доход в виде сложных процентов составит 100 000 x (1 + 0,07 x 90 / 365)2 — 100 000 = 3 481,85 рублей.
Из примеров становится понятно, что вклад со сложной ставкой значительно выгоднее, чем с простой.
Простые проценты в математике
Задача 5. В класс закупили 3 энергосберегающие окна, которые на 20 % дороже обычных. Сколько потратили денег, если за обычные окна нужно заплатить 1400 гривен.
Решение: Найдем цену энергосберегающего окнаP=1400*(1+20/100)=1680 (грн.) За три окна заплатили1680*3=5040 (грн).
Задача 6. В бочке объемом 200 литров перевозили масло . На станции отлили 60 литров. Сколько процентов от обьема осталось?
Решение: Задача состоит в нахождении количества в процентах масла от общего объема бочки.200-60=140 (л); 140/200*100%=70 % Осталось 70% объема бочки.
Задача 7. При несвоевременной уплате долгов насчитывают 2% пени за каждый просроченный день. Какую сумму нужно заплатить через 12 дней после срока погашения 500 рублей долга?
Решение: По формуле простых процентов находимP=500*(1+2/100*12)=620 (рублей)Нужно заплатить 620 рублей.
Рассмотрим задачи из учебника для 9 класса авторов А.Г. Мерзляк, В.Б. Полонский, М.С. Якир « Аглгебра ». (Номер в скобках)
Задача 8. (542) К сплаву массой 600 г, содержащему 12 % серебра, добавили 60 г серебра. Какое содержание серебра в новом сплаве?
Решение: Определяем сколько грамм серебра в первом сплавеP=600*12/100=72 (г)К найденному значению добавляем 60 грамм серебра P1=72+60=132 (г) При определении процентного содержания серебра не следует забывать, что вес нового сплава вырос на массу серебра, которую добавили. Если би Вы вычисляли следующим образом 132/600*100%=22% то получили – неправильный результат .ЗАПОМНИТЕ: в подобных задачах сначала находят меру ( вес, объем, длину) нового объекта, а затем находят содержание. В заданной задачи новый сплав получит массуP2=600+60=660 (г) а процентное содержание серебраP1/P2*100%=132/660*100%=20 % будет следующим – 20%.
Задача 9. (543) В саду росли яблони и вишни, причем яблони составляли 42% всех деревьев. Вишен было на 48 деревьев больше, чем яблонь. Сколько деревьев росло в саду?
Решение: К правильному ответу можно идти несколькими способами. Рассмотрим следующий из них. Пусть яблони составляют 42% всех деревьев, тогда вишни100-42=58%. Вишен на 48 больше нежели яблонь. Разница между ними в процентах составляет58-42=16% а в количестве – 48 деревьев. Задача состоит в нахождении количества деревьев, поэтому складываем отношения16% – 48 деревьев 100 % –Х деревьев Отсюда находим количество деревьев в садуХ=100*48/16=300 (деревьев).
Задача 10. (544) За два дня был проложен кабель. За первый день проложили 56% кабеля, а за другой – на 132 м меньше, чем первого. Сколько всего метров кабеля было проложено за два дня?
Решение: Задача похожа на предыдущую. За второй день проложили 100-56=44% кабеля, разница между первым и вторым днем составляет 56-44=12% и составляет 132 метра. На основе этого составляем отношение12% – 132 м100 % –Х м Отсюда находим искомую длинуХ=100*132/12=1100 (м.) За два дня проложили 1100 м.. кабеля.
Задача 11. (545) За первый день мальчик прочитал 25% всей книги, за второй – 72% от количества страниц что осталась, а за третий – остальные 84 страницы. Сколько страниц в книге?
Решение: 72 % процента от остатка книги составляет72*(100-25)/100= 54%. На третий день оставалось прочитать100-25-54=21% или 84 страницы. Составляем соотношение21% – 84 ст 100 % –Х ст с которого находимХ=100*84/21=400 (ст), что книга содержит 400 страниц.
Как вычисляют процентную ставку по кредиту: формулы аннуитета и дифференцированных платежей
Аннуитетные платежи предполагают погашение задолженности по займу равными платежами.
Дифференцированные платежи – это равномерное погашение основной суммы долга, но ежемесячный взнос в начале срока будет существенно больше, нежели в конце.
Расчет процентов по кредиту: аннуитетные платежи
Условие для расчета
Пусть выдано 60 000 рублей под 15% годовых на срок в 2 года, что соответствует 12 х 2 = 24 месяцам. Платеж – аннуитетный. Взносы совершаются ежемесячно.
Расчет процентов за месяц
Месячная процентная ставка составит 15% / 12 = 1,25%.
Для расчетов полученную величину переведем в десятичную дробь: 1,25% / 100% = 0,0125.
Ежемесячный аннуитетный платеж будет равен:
60 000 х 0,0125 / (1 – (1 + 0,0125) ^ (-24)) = 2 909,2 рубля.
Общая сумма к выплате за весь срок кредитования
Через 2 года заемщик заплатит:
2 909,2 х 24 = 69 820,8 рублей.
Переплата составит 69 820,8 – 60 000 = 9 820,8 рублей.
Расчет процентов по кредиту: дифференцированный платеж
Условие: первоначальные условия кредитования
Для примера расчета кредита при дифференцированном платеже воспользуемся условиями задачи, приведенной для аннуитета. Принимаем, что в среднем продолжительность месяца равна 30 дням.
Платеж в первый месяц
Формула расчета процентов по кредиту при дифференцированных платежах предполагает на первом этапе вычисление сумм, что направят на погашение основной части долга, которые будут соответствовать 60 000 / 24 = 2 500 рублям.
В 1-ый месяц платеж составит:
2 500 + 60 000 х (15% / 100%) х 30 / 365 = 2 500 + 739,73 = 3 239,73 рубля.
Выплаты второго месяца
Во 2-ой месяц остаток задолженности равен 60 000 – 2 500 = 57 500 рублей. Значит, платеж составит:
2 500 + 57 500 х (15% / 100%) х 30 / 365 = 3 208,9 рубля.
Расчет на третий месяц
Остаток к 3-ему месяцу равен 57 500 – 2 500 = 55 000 рублей, а к выплате будет:
2 500 + 55 000 х (15% / 100%) х 30 / 365 = 3 178,08 рубля.
Учитывая, что к концу срока кредитования останется 2 500 рублей, то последний месячный платеж будет равен:
2 500 + 2 500 х (15% / 100%) х 30 / 365 = 30,82 рубля.
Полный расчет ежемесячных дифференцированных платежей произведен в Excel. Переплата за все время пользования составит 9 246,58 рублей, что на 9 820,8 – 9 246,58 = 574,22 рубля меньше, нежили бы пришлось заплатить при аннуитетных платежах.
Как самостоятельно высчитать дифференцированные платежи в Excel
Просчитать дифференцированные платежи в Excel можно, составив таблицу таким образом:
- в ячейке А1 указывают «1». Так нумеруется 1-ый период кредитования;
- в А2 пишем «=А1+1» и копируем формулу до номера, соответствующего последнему месяцу кредитования. В примере это А24. Так нумеруются периоды;
- в ячейке В1 указывается первоначальная сумма займа. В примере это «60000»;
- в В2 пишется формула «=В1-М», что копируется до последнего месяца кредитования. В примере – до В24. М – это сумма кредита, разделенная на число месяцев кредитования. В примере формула примет вид «=В1-2500»;
- просчитаем месячную процентную ставку. В примере это (15%/100%) / 12 = 0,0125;
- в С1 пишем формулу для расчета дифференцированного платежа «=B1*0,0125» и копируем ее вниз до С24;
- итоговый месячный платеж формируется в столбце D путем копирования до конца таблицы формулы «=М+С1».
Какая схема расчёта процентов лучше для заемщика
Аннуитетные платежи легче переносятся семейным бюджетом, поскольку в начале кредитования они будут меньше дифференцированных. Но последний способ более экономичный.
За весь срок действия кредитного договора переплата при дифференцированных платежах будет меньше, чем при аннуитетных. Причина – скорость возврата долга при аннуитете ниже.
Исходя из структуры каждого взноса при аннуитетных платежах, очевидно, что в первое время пользования займом большая часть средств уходит на выплату процентов, и только небольшая – на погашение тела кредита.