Формула расчета аннуитетного платежа по кредиту

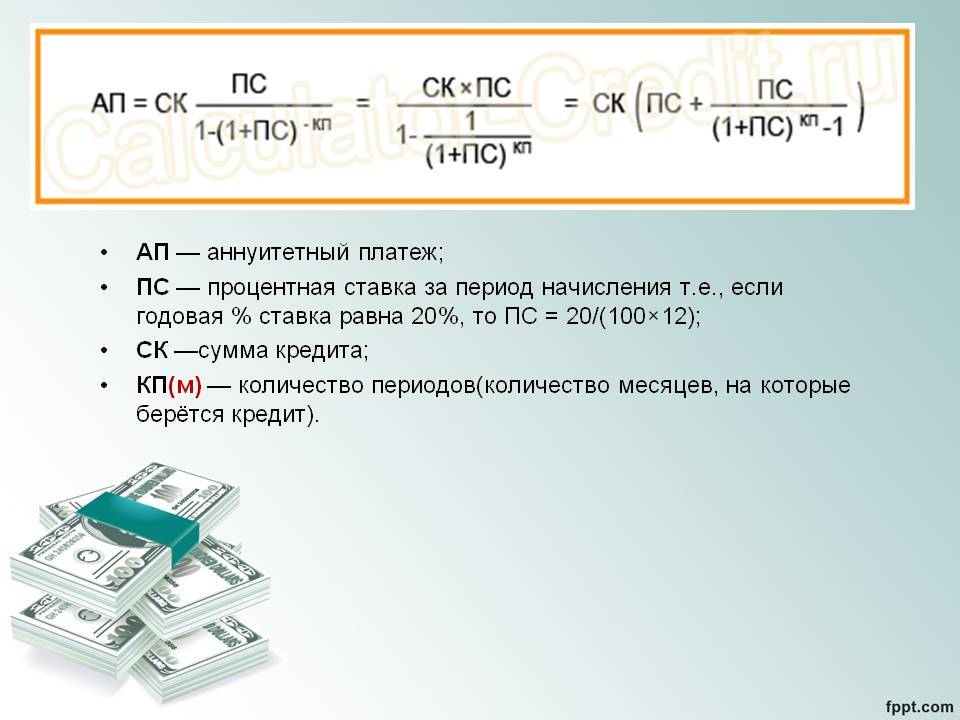
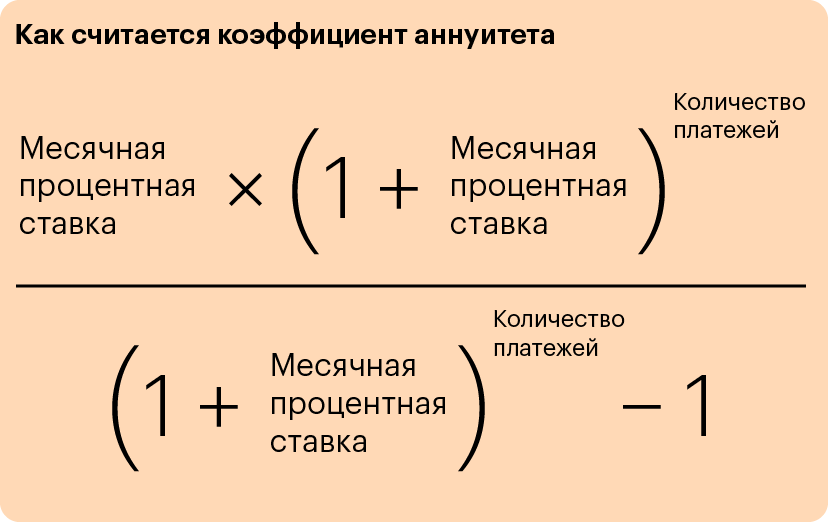
Расчет досрочного погашения при аннуитетных платежах

В случае с аннуитетными платежами используется 2 типа досрочных погашений:

1. Погашение, после которого уменьшается сумма ежемесячного платежа.
2. Погашение материнским капиталом.

Так как второй способ в основном применяется для ипотечных выплат, то остановимся на первом. Предположим, вы взяли кредит на полтора года под 15% годовых на сумму 150 000.00 рублей и в течение 2-х месяцев платили по установленному графику, а в 3-м месяце, кроме установленной суммы, внесли еще 40 000 руб. Теперь, чтобы рассчитать досрочное погашение, вам необходимо будет выполнить следующие действия:

1. Вычислить оставшуюся сумму долга по кредиту, отнять от нее сумму досрочного погашения;
2. Определить остаток срока после погашения;
3. С помощью формулы аннуитета рассчитать следующий платеж.

Вычисления:

1. Для определения остатка долга берем первоначальную сумму долга, отнимаем от нее внесенные за 3 месяца платежи «в погашение долга» и сумму досрочного погашения.

Получаем следующее: 150 000.00 — 7 482.72 — 7 576.25 — 7 670.96 – 40 000.00 = 87 270.06 руб.

1. Новый срок кредита определяется путем вычитания номера платежа от общего количества месяцев кредитования.

18 – 3 = 15. Новый срок кредита равен 15 месяцам.

1. Теперь вы имеете как бы новый кредит со следующими данными:

• S (сумма) – 87 270.06;
• N (срок) – 15 месяцев;
• Р (процентная ставка) – 15%.

Первые выплаты (до досрочного погашения) отображены в таблице:

№	Год/месяц	Всего внесено	В погашение долга	В погашение процентов	Досрочный платеж	Остаток долга после платежа
1/0	— 150 000.00	0.00	0.00	150 000.00
1	1/1	9 357.72	7 482.72	1 875.00	142 517.28
2	1/2	9 357.72	7 576.25	1 781.47	134 941.03
3	1/3	9 357.72	7 670.96	1 686.76	40 000.00	127 270.07	87 270.06

Где:

• 40 000.00 – досрочный платеж;
• 87 270.06 – остаток долга с вычетом досрочного платежа.

Чтобы определить сумму платежа после досрочного погашения, достаточно подставить полученные данные в формулу аннуитета: , но для начала надо рассчитать месячную процентную ставку: m = P:100:12 = 15:100:12 = 0,0125. Итак, наш следующий платеж будет равен 87 270.06 × = 6 416.92 Проверим свои вычисления на онлайн-калькуляторе и узнаем из полученной таблицы, которая является продолжением предыдущей, суммы последующих платежей в погашение долга и в погашение процентов:

-87 270.00	0.00	0.00	87 270.00
1	1/4	6 416.65	5 325.78	1 090.88	0.00	81 944.22
2	1/5	6 416.65	5 392.35	1 024.30	0.00	76 551.22
3	1/6	6 416.65	5 459.76	956.90	0.00	71 092.11
4	1/7	6 416.65	5 528.00	888.65	0.00	65 564.11
5	1/8	6 416.65	5 597.10	819.55	0.00	59 967.01
6	1/9	6 416.65	5 667.07	749.59	0.00	54 299.94
7	1/10	6 416.65	5 737.90	678.75	0.00	48 562.04
8	1/11	6 416.65	5 809.63	607.03	0.00	42 752.41
9	1/12	6 416.65	5 882.25	543.41	0.00	36 870.16
10	2/1	6 416.65	5 955.78	460.88	0.00	30 914.38
11	2/2	6 416.65	6 030.22	386.43	0.00	24 884.16
12	2/3	6 416.65	6 105.60	311.05	0.00	18 788.55
13	2/4	6 416.65	6 181.92	234.73	0.00	12 596.63
14	2/5	6 416.65	6 259.20	157.46	0.00	6 337.44
15	2/6	6 416.65	6 337.44	79.22	0.00	0.00

Как видите, разница лишь в копейках. Из приведенных примеров можно сделать вывод, что досрочное погашение аннуитета не так уж и выгодно, поскольку при определении новой суммы долга вычитаются только платежи в погашение долга, а те, которые идут на погашение процентов (а они как раз в начале кредитования – максимальные) просто дарятся банку. В некоторых банках все же можно получить переплаченные проценты, но они пересчитываются уже при окончательном закрытии кредита (когда есть возможность установить реальный срок пользования деньгами).

Плюсы и минусы аннуитетной схемы погашения платежей

Какие же может иметь выгоды аннуитетный платеж – в чем его преимущество? Основными плюсами такого метода являются следующие:

• По сравнению с дифференцированной схемой первая половина аннуитетных платежей будет значительно меньшей по размеру;
• Оформляя подобный вид кредита, заемщик заранее знает положенную сумму платежа, которая не будет изменяться с течением времени. Таким образом гораздо легче планировать распределение личного или семейного бюджета;
• Данный способ идеально подходит для оформления больших сумм кредитов, поскольку банковские организации могут рассчитать ежемесячный платеж, исходя их постоянного среднемесячного дохода кредитора;
• Если у клиента банка имеется возможность оформления налогового вычета по покупке квартиры, то сумма, которую он получит, будет большей, нежели по дифференцированной схеме.

Недостатком аннуитетной схемы является то, что в итоге заемщик выплачивает по кредиту большую сумму, чем пришлось бы перечислить при дифференцированном способе. Почему же люди все таки выбирают такую схему, ведь они понимают, что придется отдать больше? Основной причиной является то, что при оформлении кредита с дифференцированным способом погашения у должника просто может не хватать средств на выплату первых взносов – ведь их размер может быть очень значительным.  Поэтому, хоть аннуитетный способ и ведет к некоторым переплатам, но человек в итоге получает необходимую сумму денег в долг и имеет реальную возможность его вернуть, постепенно перечисляя небольшие платежи.

Таким образом, аннуитетная схема кредитования предполагает погашение долгового обязательства в равных суммах каждый месяц. Рассчитать размер взносов можно самостоятельно по приведенной нами формуле, либо же воспользовавшись специальным калькулятором.

Какой лучше выбрать способ погашения взятого кредита

Многие заемщики не знают, что значит аннуитетный способ погашения и не выделяют его отличия от дифференцированного. Однако, если бы они подсчитали получившуюся переплату, то поняли бы, что при дифференцированном способе она получается несколько меньше.

С одной стороны, дифференцированные выплаты по кредиту выгодны, так как размер долга получается меньше. Кроме того, при такой схеме последующие платежи меньше предыдущих. При досрочном же погашении кредита с такими условиями значительно экономятся выплачиваемые проценты.

Аннуитетные и дифференцированные платежи

С другой стороны, аннуитет выгоден тем, у кого сразу нет большой суммы для погашения большого размера задолженности, как это бывает при дифференцированных платежах в первые месяцы. Однако в первой половине времени гашения, задолженность почти не закрывается, ведь идет выплата начисленных сверху процентов. В итоге ежемесячные платежи невелики, но общий размер денег, которые заемщик отдаст банку, увеличивается.

Аннуитетный платеж – что это такое для финансовой организации? Выгодный финансовый инструмент, используемый при кредитовании. Некоторым банкам бывает неудобно при таком способе закрывать погашения кредита досрочно. В итоге определяется минимальный размер досрочного погашения и срок.

Если же провести скрупулезный подсчет переплаты по кредиту с первым и вторым рассмотренным способом погашения, можно увидеть, что не такое уж и сильное дифференцированные платежи дают преимущество. Если уж у заемщика и есть возможность погашения большей части суммы дифференцированных платежей в первый, самый тяжелый по выплачиваемым процентам год, то и аннуитетные платежи он будет вполне в состоянии выплачивать. К тому же при равномерном погашении максимальный размер кредита может быть больше, условия по процентным ставкам – лояльнее, а срок погашения – ниже. В этом заключается неоспоримое преимущество таких ежемесячных выплат.

Составляющие ежемесячного платежа

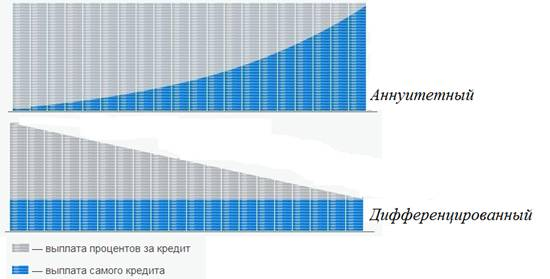
Аннуитетный платеж является самым распространенным вариантом ежемесячных выплат по кредитам. Клиент каждый месяц вносит на счет банка, независимо от величины оставшейся задолженности, фиксированную сумму, состоящую из двух частей: тело кредита и процентная ставка.

Это отличает аннуитет от дифференцированного варианта выплаты, где в начале кредитного периода большая часть вносимой суммы — проценты. Основной долг уменьшается медленно, а размер переплаты значительно увеличивается.

Рассчитать сумму ежемесячных выплат можно с помощью кредитного калькулятора, который можно найти на официальных сайтах практически всех банков: Сбербанка, ВТБ, Альфа и прочих.

Используя форму онлайн-расчетов можно узнать суммы, которые идут на погашение долга и процентов.

Но расчеты, выполненные самостоятельно по формуле, дадут более точный результат.

Расчёт процентов по аннуитетным платежам

Посчитать долю процентов в аннуитетных платежах вам поможет вот эта формула:

Давайте для наглядности рассчитаем долю процентов в первом платеже по нашему кредиту:

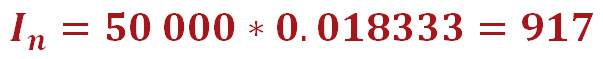
Так как это первый платёж, то суммой оставшейся задолженности по кредиту является весь кредит – 50 000 руб. Умножив эту сумму на ежемесячную процентную ставку – 0.018333, мы и получим 917 руб. – сумму, указанную в нашем графике.

При расчёте суммы процентов в следующем аннуитетном платеже, на месячную процентную ставку умножается долг, который сформировался на конец предыдущего месяца (в нашем случае это 46 237 руб.). В результате получится 848 руб. – размер доли процентов во втором аннуитетном платеже. По такому же принципу рассчитываются проценты в остальных платежах. Далее давайте вычислим составляющую в аннуитетных платежах, которая пойдёт на погашение тела кредита.

Советы и рекомендации по выгодному погашению банковских долгов

Главный совет: не берите банковские займы без особой нужды. Если все же решили прокредитоваться, подумайте, сможете ли рассчитываться по взятым обязательствам не только сейчас, но и в будущем.

Если у заемщика несколько кредитов, то, как показывает практика, при появлении свободных средств он старается гасить досрочно самый дорогой кредит.

Мы же рекомендуем направить «досрочку» на погашение займа с наименьшим ежемесячным платежом. Так вы быстрее с ним рассчитаетесь, а высвободившиеся средства сможете направить на дополнительную оплату следующего в очереди обязательства.

Например:

Вид кредита	Сумма (руб.)	Ставка (%)	Платеж (руб.)	Очередь для досрочного погашения
Потребкредит	350000	17	8700	2
Автокредит	150000	9	3200	1

Внося дополнительно в уплату автокредита, например, 2000 руб. в месяц, вы закроете его на 2 года 7 месяцев раньше. Направив эту же сумму на досрочное гашение более дорогого потребкредита, ускорите его выплату лишь на 1 год.

Закрыв очередной кредит, не тратьте высвободившиеся деньги на текущие расходы, а направляйте их на выплаты по оставшимся займам.

Отслеживайте условия по аналогичным предложениям. Возможно, ставки снизились, и вам будет выгодно перекредитоваться. Даже снижение ставки, действующей по текущему обязательству, на 1% даст существенную экономию.

Досрочное погашение

Практически каждого клиента интересует вопрос досрочного погашения кредита. Раньше банки составляли кредитные договора так, что при досрочном погашении взималась какая-либо комиссия или штраф за неустойку и прочее. Однако же теперь, в соответствии с законодательством все крупнейшие российские банки «разрешают» клиенту закрывать долг досрочно полностью или частично.

Итак, что же меняется при досрочном погашении кредита? Будет ли при этом меняться процент по кредиту и изменяться график ежемесячных платежей?

Как правило, при досрочном частичном погашении кредита процентная ставка, изначально прописанная в договоре, не меняется. После списания средств, возможно только изменение графика платежей (на сокращение срока или уменьшение ежемесячного платежа).

Если сравнить аннуитетную систему выплат и дифференцированную, то, однозначно, по последней – при частично досрочном погашении задолженности, клиент «выиграет» куда больше, нежели с аннуитетом. Так как досрочно спишется большая часть его основного долга, нежели проценты за пользование кредитными средствами.

К слову! Хочется заметить, что после частично досрочного погашения любого кредита, банковская программа автоматически меняет график платежей (причем ставка остается та же).

Многим кажется, что после данной операции наперед сумму ежемесячных платежей самостоятельно просчитать будет сложнее, чем при получении кредита изначально. Однако, это миф. Считается все ровно по тем же схемам. Только за вычетом уже погашенной задолженности. Напоминаем, что при дифференцированной системе клиент всегда экономит больше, чем при аннуитете, несмотря на его «удобность».

Досрочное погашение кредита при аннуитетном платеже

Зачастую сомнения относительно выгоды аннуитетных платежей связаны с возможностью досрочного погашения кредита. Так как сумма по аннуитету является фиксированной, то появляется вопрос о том, что делать с выплатой процентов. При этом нужно выбрать полное или частичное погашение кредита.

При дифференцированном платеже с досрочным погашением все просто, а вот при аннуитетном могут быть использованы только два метода частичного погашения:

• С уменьшением срока;
• С уменьшением ежемесячного платежа.

При уменьшении срока процентный выплаты также уменьшаются, но нагрузка по самому долгу увеличивается. Во втором случае уменьшается сам размер ежемесячных выплат, сроки дольше, а проценты становятся лишь немного меньше. Сокращение срока кредитования позволяет сэкономить на выплатах по процентам, однако контролировать расходы проще с уменьшением платежей.

Также при аннуитетном платеже важно обратить внимание на вид досрочного погашения. Если планируется полное, то и формула расчета будет другой. Независимо от выбранного метода погашения схема действий одинаковая:

Независимо от выбранного метода погашения схема действий одинаковая:

1. В банке пишется заявление с просьбой о досрочном погашении;
2. При принятии и подтверждении банк предлагает соответствующий вид досрочного погашения;
3. Вносятся соответственно полная сумма по кредиту и проценты или новая установленная сумма;
4. В случае, если погашение полное, то выдается справка о выплате кредита;
5. Происходит возврат средств по страховке, если таковая была навязана.

Важно помнить, что в зависимости от банка, в котором происходило кредитование, клиенту могут не предложить выбор, так как в самой системе банка используется только конкретный вид выплат при досрочном погашении аннуитетного платежа. Популярные вопросы по статье

В чем главное отличие аннуитетных платежей по кредиту от дифференцированных?

Популярные вопросы по статье

В чем главное отличие аннуитетных платежей по кредиту от дифференцированных?

При аннуитетных формах выплат ежемесячная сумма платежей является одинаковой на протяжении всего периода кредитования, что позволяет существенно снизить финансовую нагрузку на клиента.

Чем выгодны аннуитетные платежи по кредитам для клиентов?

Преимущество аннуитетных платежей в том, что ежемесячно выплачивается фиксированная сумма, которая точно известна заемщику. При дифференцированных выплатах приходится выяснять сумму выплат каждый месяц заранее.

Можно ли досрочно погасить кредит с аннуитетным видом платежей?

При аннуитетных платежах возможно погасить кредит досрочно целиком или частично. При этом банк может не предоставлять выбор в виде частичных выплат.

Кому подойдут кредиты с аннуитентными платежами?

Кредит с аннуитентными выплатами наиболее удобен людям, у которых четкое распределение бюджета. Однако при этом лучше, чтобы доход был выше среднего, так как общая переплата по кредиту будет больше, чем при дифференцированных платежах.

Похожие

• Как оплатить кредит ОТП банка онлайн: все способы
• Карта “Халва”: условия рассрочки, плюсы, минусы
• Как проверить баланс на карте Сбербанка через телефон по СМС
• Как перевести деньги с МТС на карту Сбербанка
• Как взять доверительный платеж на Мегафоне
• Горячая линия Сбербанка 8(800)555-55-50: бесплатный телефон техподдержки
• Как отключить копилку в Сбербанк Онлайн
• Как рефинансировать кредит в Тинькофф банке?
• Как узнать баланс карты Сбербанка. 7 способов проверить баланс карты
• Рефинансирование ипотеки: особенности, преимущества, недостатки, выгодные предложения

Онлайн-калькулятор

Все вышеприведённые вычисления на многих обывателей наводят тоску и даже ужас. Потому, чтобы не страдать лишний раз, придумали онлайн-калькуляторы. С их помощью можно быстро рассчитать всё то, что мы учились в статье считать вручную.

Как пользоваться?

Алгоритм использования таких сервисов донельзя прост. Какой бы калькулятор Вы не выбрали, для начала нужно подготовить известные из договора сведения.

Сумма займа, срок кредитования, число/месяц/год выдачи заёмных средств, процентная ставка – всё необходимо иметь перед глазами. Если Вы не помните эту информацию наизусть, откройте соглашение, которое было заключено с банком: в документе прописаны абсолютно все нюансы сотрудничества и эксплуатации кредита.

Указанные данные следует внести в поля калькулятора. Проследите за корректностью вводимых значений.

В завершение останется лишь нажать кнопку “Рассчитать” (названия опции могут быть разными – всё зависит от выбранного сервиса – но смысл сохраняется)

Система выдаёт результат мгновенно.

Расчёт аннуитетного платежа

Теперь рассмотрим порядок действий на конкретном примере.

Используем калькулятор с сайта calcus.ru.

Что нужно сделать:

• в окошко “Сумма кредита” внесите размер взятых в заём средств;
• укажите период кредитования в окне “Срок кредита” – при этом выберите лучше месяцы вместо годичного обозначения;
• ниже впишите дату, когда вы получили займ, в формате ДД.ММ.ГГ;
• в выпадающем меню категории “Процентная ставка” выберите пункт “Постоянная”, а правее введите значение;
• “Вид платежа” – отмечаем “Аннуитетный”;
• укажите, когда по договору положено вносить ежемесячный платёж (в конце месяце или в начале – какого числа, в день выдачи займа и т.д.);
• кликните по кнопке “Рассчитать”.

Сервис тут же выдаст итог: размер ежемесячного платежа и переплату по кредиту.

На все манипуляции времени уходит меньше минуты.

Обратите внимание: мы использовали все те значения, что применялись ранее при ручных расчётах. Имеется некоторое разночтение

Это зависит от того, какую погрешность задаёт калькулятор. Мы были точны до десятитысячной доли. В любом случае самостоятельные вычисления нужны для лучшего ориентирования в расходах.

Примечание 3. Итоги расчётов, проведённых самостоятельно, могут отличаться от тех, что выдадут в банке. Отслеживайте эти нюансы и тщательно консультируйтесь, преждем чем оформлять займ.

Аннуитетный платёж

Любой банк при выдаче займа гражданину имеет доход прежде всего с выплачиваемых процентов. По этой причине компания предпочитает, чтобы клиент выплачивал долг подольше, при этом покрывая сначала именно проценты.

Аннуитетная форма погашения займа – как раз то, что нужно банку.

Что подразумевает под собой этот платёж? Покрытие задолженности происходит равными частями. Конечно, это имеет свой плюс для клиента: ему нужно раз в месяц вносить относительно небольшую сумму в счёт кредита. Т.к. обычно граждане не имеют возможности выделять крупные объёмы средств на те или иные цели, аннуитет тут очень кстати.

В чём же конкретно состоит выгода банковской организации? Дело в том, что при равных выплатах по аннуитетной форме сначала покрывается не тело займа.

Важно! Расчёт организуется так, что большая часть средств уходит на погашение постоянно начисляемых процентов, в то время как сам долг покрывается меньшей частью вносимых денег.

Указанные моменты обеспечивают более высокую финальную стоимость кредита. Всё из-за медленного процесса выплат. Чем дольше платишь – тем большая сумма уйдёт на покрытие задолженности.

Формула расчета платежа

Существует специальная формула расчета кредита:

При этом:

• Х — ежемесячный аннуитетный платеж;
• S — тело кредита;
• m — процентная ставка банка (ежемесячная), установленная на сумму займа
• N — количество процентных периодов (месяцев).

Зная формулу расчета выплат, очень просто узнать точную сумму аннуитетного платежа. Например: в банке взят кредит на 2 года, в сумме 20 000 руб. Годовая процентная ставка составляет 22%. Как рассчитать ежемесячный взнос?

Месячная процентная ставка вычисляется по формуле m=P/100/12, где Р-годовая процентная ставка финансового учреждения. В данном случае Р=22%, значит

• m = P/100/12 = 22:100:12 = 0,0183;
• S = 20 000;
• N = 24.

Подставив данные в формулы, получаем:

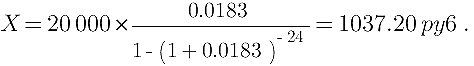
То есть, клиент в течение 2 лет должен каждый месяц платить банку 1037 руб. 20 коп.

Очень просто подсчитать переплату по кредиту: 1 037.20 х 24-20 000 = 4 892.80. Сумма переплаты по кредиту составит 4 892.80 руб.

Калькулятор кредитного платежа, существующий на сайте Сбербанка и других финансовых учреждений, покажет такой же результат. Возможные отличия объясняются округлением полученных сумм или разными процентными ставками.

Пример расчета

Предположим, что нужно провести расчёт ежемесячного платежа по кредиту с аннуитетным графиком погашения под процентную ставку 48% годовых сроком на 4 года на сумму 20 000 000 рублей. Используя приведённую выше формулу расчёта ежемесячного платежа (A = K • S) и коэффициента К, рассчитаем аннуитетный платёж.

Имеем:

1. i= 48%/12 месяцев = 4% или 0,04
2. n = 4 года* 12 месяцев = 48 (месяцев)
3. S = 20 000 000

А = 0,0472 * 20 000 000 = 943 613 рублей.

Таким образом, в течение 4 лет (или 48 месяцев) необходимо будет вносить в банк платёж в сумме 943 613 рублей. Переплата по кредиту за 4 года составит 25 293 422 ( = 943 613 * 48 – 20 000 000).

В первую очередь аннуитетный способ погашения выгоден банку.

Объясняется это тем, что в течение всего срока погашения кредита проценты начисляются на первоначальную сумму кредита. При дифференцированной графике уплата процентов за 100% суммы кредита происходит только в первом месяце (в случае отсутствия отсрочки уплаты основного долга), далее проценты начисляются на остаток, из-за чего итоговая переплата по кредиту окажется меньше.

Для примера, рассчитаем переплату по кредиту, рассмотренному выше, но теперь с дифференцированным графиком погашения. Она составит 19 600 000 рублей. Это на 5 693 422 рубля меньше, чем при аннуитетной схеме.

С другой стороны, погашение задолженности и процентов равными долями удобно кредитополучателю.

Так как ежемесячный платёж является постоянным и не требует уточнения в банке необходимой суммы взноса.

Применение аннуитетного способа погашения, таким образом, обойдётся дороже, но при этом гораздо удобнее.

Теперь давайте попробуем рассчитать ипотеку. Для примера возьмем займ со следующими параметрами

Параметры рассчитываемого кредита
Сумма	1 млн рублей.
Ставка	12%
Срок	60 месяцев
Дата первого платежа	1 сентября 2011.

где Погашение ОД — сумма в погашение тела займаПроценты — сумма процентов по ссуде за месяц.Где сумма ОД — сумма основного долга на дату расчета.Ставка — процентная ставка в текущем периоде. Если было изменение процентной ставки, берется новая ставка.Число дней между датами — разность в днях между датами «Дата текущего платежа» и дата предыдущего платежа.

В нашем примере при первом платеже это делать не нужно.Рассчитаем первый платеж в уплату процентов по указанному выше займу за сентябрь месяц(разнца между датами 31 день).Как видно сумма ОД на первый месяц составляет 1 млн. рублей. Подставим даты, ставки и число дней в году.

Как видно, в счет уплаты процентов должно пойти 10191.78Произведем расчет суммы в погашение тела займа

Теперь рассчитаем сумму основного долга после оплаты первого взноса по ипотеке

Теперь допустим, мы погасили 100000 рублей в августе 2012. Тип погашения — в уменьшение суммы займа. Т.е срок останется тем же, а ежемесячный платеж уменьшится.Попробуем посчитать, сколько будет составлять платеж после учета досрочных погашений. В октябре будет уже новый платеж по займу с учетом досрочки.

Воспользуемся формулой для расчета аннуитетных платежей. Из всех параметров у нас изменилась только сумма основного долга после досрочного погашения в августе она равна

Вычисленная выше сумма и будет сумма кредита после досрочного погашения.Именно исходя из этой суммы и будет рассчитываться ежемесячный аннуитетный платеж после досрочного погашения.

Очевидно срок кредита также изменится, нужно отнять от общего срока число месяцев, прошедшее до досрочного погашения с момента выдачи займа.

Подставим новую сумму в формулу аннуитетного платежа получим новый платеж по займу.

Итоговый расчет

Проверим это с помощью программы кредитный калькулятор

Как видно результат полностью совпадает. Также можно воспользоваться онлайн версией кредитного калькулятора. Там используется указанная выше формула аннуитетного платежа. График кредитного калькулятора может быть использован для сверки расчетов вашего кредита с расчетом банка. Иногда данные могут не совпасть.

Вот к примеру форумла аннуитета в банке ЛевобережныйПо формулеФормула немного другая. Она взята из стандартного ипотечного договора.Вы должны понимать, что досрочное погашение с финансовой точки зрения не всегда выгодно. Предлагаю попробовать калькулятор, определяющий выгодность досрочного погашения.

Способы расчета суммы кредита с помощью Excel-таблицы

Размер платежа зависит от способа исчисления. Современные отечественные банки применяют два способа расчета: аннуитетный и дифференцированной. В каждом из них имеется тело кредита и начисляемые проценты. Оба типа можно включить в Excel-таблицу, где заранее будут прописаны формулы.

Для расчета платежей по кредиту используется специальная формула

Аннутитетные платежи

В 2019 году российские банки для оформления кредитов берут чаще всего аннуитетные системы, которые подразумевают ежемесячные выплаты по кредиту, при этом вносимая заемщиком сумма не изменяется на протяжении всего периода кредитования. Такая практика пришла к нам из Европы, где банкиры успели ее оценить по достоинству.

Размер регулярного взноса принято рассчитывать по формуле:

Е = К * S, где

Е — месячный платеж;

К — коэффициент аннуитетного платежа;

S — первоначальная сумма задолженности.

Для расчета коэффициента можно применять такую зависимость:

К = (j * (1 + j)^m) / ((1+j)^m-1), где

j — ежемесячная ставка процентов, которая высчитывается при делении годовой на 12 (кол-во месяцев в году);

m — период кредитования в месяцах.

В таблице расчетов процентов по кредиту для эксель можно применять стандартную формулу аннуитета. Для этого используется аббревиатура ПТЛ:

• вносим входные параметры для расчета месячных взносов по кредиту;
• формируем график погашения с колонками «Номер месяца» и «Платеж»;
• для первой ячейки «Платеж» прописываем формулу =ПЛТ($B$3/12; $B$4; $B$2);
• можно заменить ссылки константными данными, тогда пример будет выглядеть таким образом =ПЛТ(12%/12; 24; 1000000).

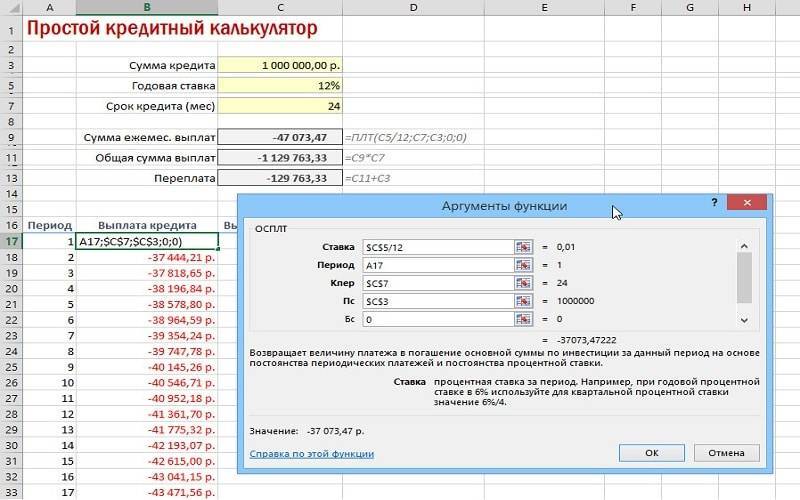
В полях «Платежи» значения примут красный цвет и будут отрицательными. Это связано с тем, что суммы нужно будет отдавать.

Дифференцированная схема

Проводить расчеты потребительского кредита в Эксель можно по дифференцированному принципу. Суть дифференцированных платежей заключается в том, что во время погашения уменьшается остаток долга, на который начисляются проценты. Соответственно месячный платеж постоянно снижается. Фактически долг распределяется равномерно по всему периоду, а процентный платеж, уплачиваемый ежемесячно на остаток, становится меньше, за счет чего снижается общая сумма месячного платежа.

Так как формулы расчета аннуитетного и дифференцированного платежа по кредиту в Excel отличаются, то приведем ее для второго типа:

МП = ОСЗ / (ПП + ОСЗ * МС), где

МП — месячный кредитный платеж;

ОСЗ — сумма остатка тела кредита;

ПП — количество периодов до полного погашения;

МС — ежемесячная ставка процентов, которая вычисляется делением годовой на 12 месяцев.

Для первого месяца задолженность по кредиту составит =$B$2. Дальнейшие оплаты со второй включительно необходимо рассчитывать по формуле в таблицах эксель =ЕСЛИ(D10>$B$4;0;E9-G9). В данной зависимости под D10 скрывается номер периода, под В4 время кредита, в Е9 вносится остаток от предыдущего периода, а G9 – размер основной задолженности в прошлом периоде. При сравнении одинаковых сумм и времени погашения будет такой результат.

Очевидно, что в черном цвете дифференцированный способ выгодней для клиента. При его расчете оказывается меньшая переплата.

Пример расчета

К_А = ( 0,02*(1+0,02)12 ) / ( (1+0,02)12 – 1 ) = ( 0,02 * 1,27 ) / ( 1,27 — 1) = 0,09407

А_П = 0,09407 * 100000 = 9407 рублей.

А_п год = 9407 * 12 = 112884 рубля. Таким образом, плата за использование кредитных средств составила 12884 рубля, эффективная ставка по кредиту 12,88%.

А_п = 100000 * (0,02 / (1 – (1+0,02)-12 )) = 100000 * (0,02 / (1 – 1/1,27) = 100000 * 0,09412 = 9412 рублей.

А_п год = 9412 * 12 = 112944 рубля. Таким образом, плата за использование кредитных средств составила 12944 рубля, эффективная ставка по кредиту 12,94%.

Очевидно, что каждая формула даст немного другой результат. Чем больше будет сумма кредита, тем существеннее расхождение в величинах аннуитетного платежа.

В данном видео рассказано в каком случае лучше выбирать аннуитетные платежи по кредиту, а в каком — дифференцированные:

Что такое аннуитетные платежи

к равномерным платежам в течение всего периода

Основным отличием аннуитета от дифференцированного платежа является периодичность, в то время как дифференцированный платеж характеризуется выплатой основной суммы долга в конце периода.

В широком смысле под аннуитетом понимается график погашения долга, систему равномерных платежей и даже величину, которую периодически выплачивает застрахованное физическое лицо.

В российских страховых компаниях и коммерческих банках наиболее распространен именно этот тип платежей. Данный термин также применяется для равномерных взносов на сберегательный счет (депозит) с целью накопления определенной суммы.

Существуют два типа аннуитетного платежа – постнумерандо (первая выплата происходит в конце начального периода) и пренумерандо (первая выплата происходит в начале нулевого периода). Постнумерандо является более распространенным и удобном способом, поэтому используется коммерческими банками при кредитовании.

Несмотря на то, что аннуитет считается неизменным платежом, его структура меняется от периода к периоду. Аннуитет, оплаченный в первые месяцы преимущественно состоит из процентов по кредиту и в меньшей степени из суммы основного долга. в конце периода кредитования ситуация меняется – аннуитет практически полностью состоит из платежей по основному долгу.

Основная формула аннуитетного платежа в Excel

Как и говорилось выше, в Microsoft Office Excel можно работать с различными типами платежей по кредитам и ссудам. Аннуитет не является исключением. В общем виде формула, с помощью которой можно быстро вычислить аннуитетные взносы, выглядит следующим образом:  

Основные значения формулы расшифровываются так:

• АП – аннуитетный платеж (название сокращено).
• О – размер основного долга заемщика.
• ПС – процентная ставка, выдвигаемая ежемесячно конкретным банком.
• С – число месяцев, на протяжении которых длится кредитование.

Для усвоения информации достаточно привести несколько примеров использования данной формулы. О них пойдет речь далее.

Примеры использования функции ПЛТ в Excel

Приведем простое условие задачи. Необходимо посчитать ежемесячный кредитный платеж, если банк выдвигает процент в размере 23%, а общая сумма составляет 25000 рублей. Кредитование продлится на протяжении 3-х лет. Задача решается по алгоритму:

1. Составить общую таблицу в Excel по исходным данным.

1. Активировать функцию ПЛТ и ввести для нее аргументы в соответствующее окошко.
2. В поле «Ставка» прописать формулу «В3/В5». Это и будет процентная ставка по взятому кредиту.
3. В строке «Кпер» написать значение в виде «В4*В5». Это будет общее количество выплат за весь срок кредитования.
4. Заполнить поле «Пс». Здесь нужно указать первоначальную сумму, взятую в банке, прописав значение «В2».

Необходимые действия в окне «Аргументы функции». Здесь указан порядок заполнения каждого параметра

1. Удостовериться, что после нажать «ОК» в исходной таблице посчиталось значение «Ежемесячный платеж».

Финальный результат. Ежемесячный платёж посчитан и выделен красным цветом

Пример расчета суммы переплаты по кредиту в Excel

В этой задаче надо подсчитать сумму, которую переплатит человек, взявший кредит 50000 рублей по процентной ставке 27% на 5 лет. Всего в год заемщик производит 12 выплат. Решение:

1. Составить исходную таблицу данных.

Таблица, составленная по условию задачи

1. Из общей суммы выплат отнять первоначальный размер суммы по формуле «=ABS(ПЛТ(B3/B5;B4*B5;B2)*B4*B5)-B2». Ее надо вставить в строку формул сверху главного меню программы.
2. В итоге в последней строке созданной таблички появится сумма переплат. Заемщик переплатит 41606 рублей сверху.

Финальный результат. Практически двукратная переплата

Формула вычисления оптимального ежемесячного платежа по кредиту в Excel

Задача с таким условием: клиент зарегистрировал счет в банке на 200000 рублей с возможностью ежемесячного пополнения. Нужно посчитать количество платежа, который человек должен вносить каждый месяц, чтобы через 4 года на его счету оказалось 2000000 рублей. Ставка составляет 11%. Решение:

1. Составить табличку по исходным данным.

Таблица, составленная по данным из условия задачи

1. В строку ввода Эксель ввести формулу «=ПЛТ(B3/B5;B6*B5;-B2;B4)» и нажать «Enter» с клавиатуры. Буквы будут отличаться в зависимости от ячеек, в которых размещена таблица.
2. Проверить, что сумма взноса автоматически посчиталась в последней строке таблицы.

Окончательный результат расчета

Особенности использования функции ПЛТ в Excel

В общем виде данная формула записывается следующим образом: =ПЛТ(ставка; кпер; пс; ; ). У функции есть следующие особенности:

Когда рассчитываются ежемесячные взносы, в рассмотрение берется исключительно годовая ставка.
Указывая размер процентной ставки, важно сделать перерасчет, опираясь на число взносов за год.
Вместо аргумента «Кпер» в формуле указывается конкретное число. Это период выплат по задолженности.

Заключение

Важно! Все пункты условия кредитования в каждой кредитной организации четко прописаны. Кредитный договор по закону не может иметь скрытые платежи или комиссии без указания таковых на страницах документа

• Сумма: до 5 000 000 ₽;
• Срок: до 5 лет;
• Процентная ставка: от 11,9%
• Решение: от 2 минут.
• ️ Получить деньги

• Сумма: до 5 000 000 ₽;
• Срок: до 5 лет;
• Процентная ставка: от 6,5%
• Решение: до 2 минут.
• ️ Получить деньги

• Сумма: до 2 000 000 ₽;
• Срок: до 3 лет;
• Процентная ставка: от 8,9%
• Решение: от 1 минуты.
• ️ Получить деньги

• Сумма: до 5 000 000 ₽;
• Срок: до 7 лет;
• Процентная ставка: от 7,5%
• Решение: до 5 минут.
• ️ Получить деньги

• Сумма: до 1 500 000 ₽;
• Срок: до 5 лет;
• Процентная ставка: от 5,9%
• Решение: от 1 минуты.
• ️ Получить деньги

• Сумма: до 5 000 000 ₽;
• Срок: до 5 лет;
• Процентная ставка: от 6,9%
• Решение: от 15 минут.
• ️ Получить деньги

• Сумма: до 5 000 000 ₽;
• Срок: до 7 лет;
• Процентная ставка: от 5,9%
• Решение: индивидуально.
• ️ Получить деньги

• Сумма: до 2 000 000 ₽;
• Срок: до 5 лет;
• Процентная ставка: от 7,99%
• Решение: до 2 минут.
• ️ Получить деньги

• Сумма: до 3 000 000 ₽;
• Срок: до 5 лет;
• Процентная ставка: от 9,5%
• Решение: до 3 дней.
• ️ Получить деньги

• Сумма: до 1 000 000 ₽;
• Срок: до 5 лет;
• Процентная ставка: от 17,9%
• Решение: индивидуально.
• ️ Получить деньги

• Сумма: до 5 000 000 ₽;
• Срок: до 5 лет;
• Процентная ставка: от 6,9%
• Решение: от 5 минут.
• ️ Получить деньги

• Сумма: до 3 000 000 ₽;
• Срок: до 7 лет;
• Процентная ставка: от 5,5%
• Решение: от 5 минут.
• ️ Получить деньги

• Сумма: до 3 000 000 ₽;
• Срок: до 7 лет;
• Процентная ставка: от 8,99%
• Решение: от 15 минут.
• ️ Получить деньги

• Сумма: до 4 000 000 ₽;
• Срок: до 7 лет;
• Процентная ставка: от 10,5%
• Решение: от 1 минуты.
• ️ Получить деньги

• Сумма: до 3 000 000 ₽;
• Срок: до 5 лет;
• Процентная ставка: от 7,9%
• Решение: от 2 минут.
• ️ Получить деньги

• Сумма: до 3 000 000 ₽;
• Срок: до 5 лет;
• Процентная ставка: от 8,9%
• Решение: от 1 минуты.
• ️ Получить деньги

• Сумма: до 300 000 ₽;
• Срок: до 5 лет;
• Процентная ставка: от 10,5%
• Решение: до 1 минуты.
• ️ Получить деньги